CAT 2018 Set-2 | Question: 74

Question

Let $f\left (x  \right ) = \max\left \{5x, 52 – 2x^{2}\right \}$ , where $x$ is any positive real numbers. Then the minimum possible value of $f(x)$ is ________

Answer 1

Given that, $ f(x) = \max \{ 5x, 52-2x^{2} \} \quad \longrightarrow (1) $

And, $x$ is a positive real number.

The minimum value occurs when both the graphs intersect.

• Let $ y_{1} = 5x \quad \longrightarrow (2) $
• And, $ y_{2} = 52 – 2x^{2} \quad \longrightarrow (3) $

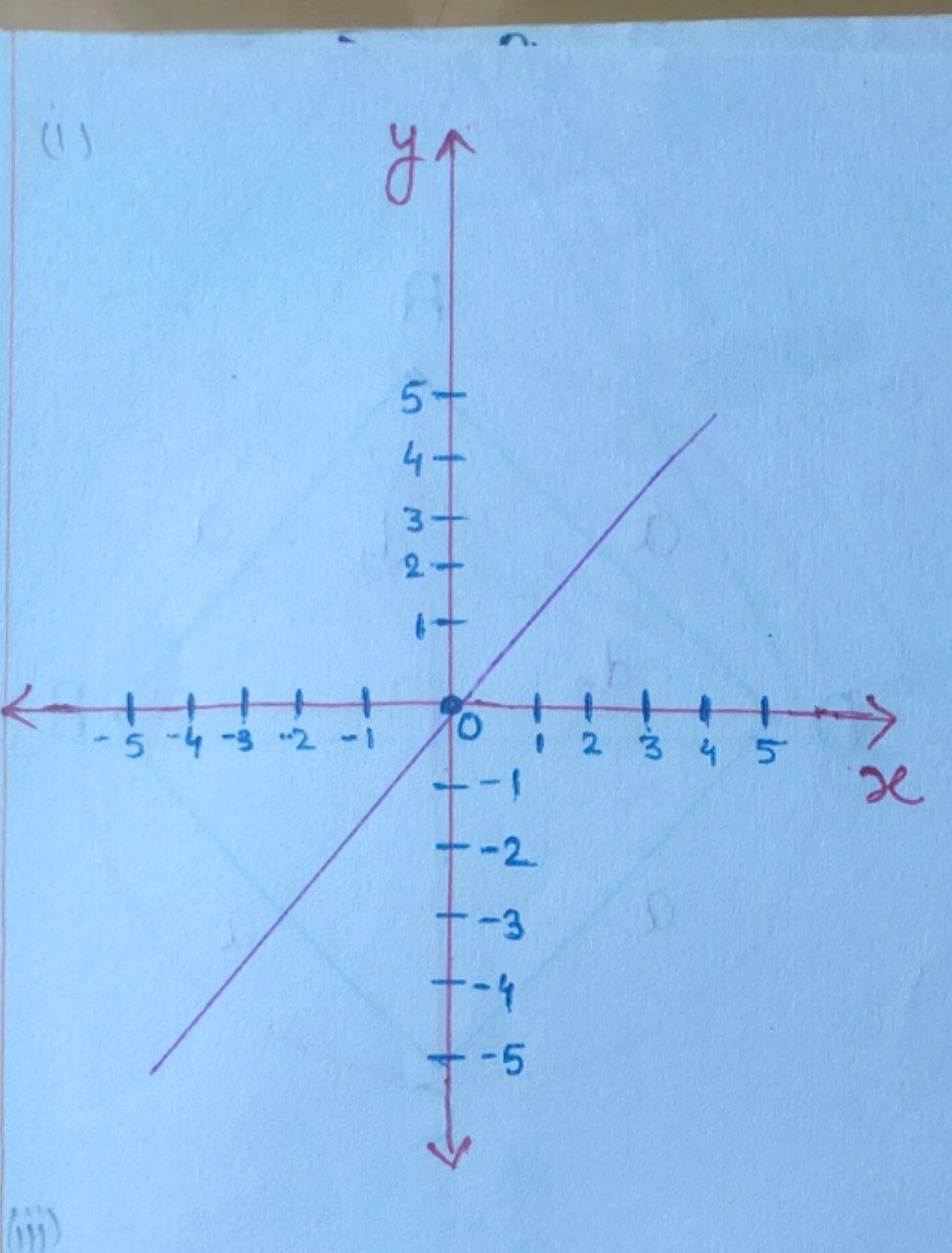
From equation $(2),$

$ y_{1} = 5x$ is an equation of line.

$ y = mx+c\,,$ where $m =$ slope of the line , $c =$ intercept on the $y$ – axis.

From equation $(3),$

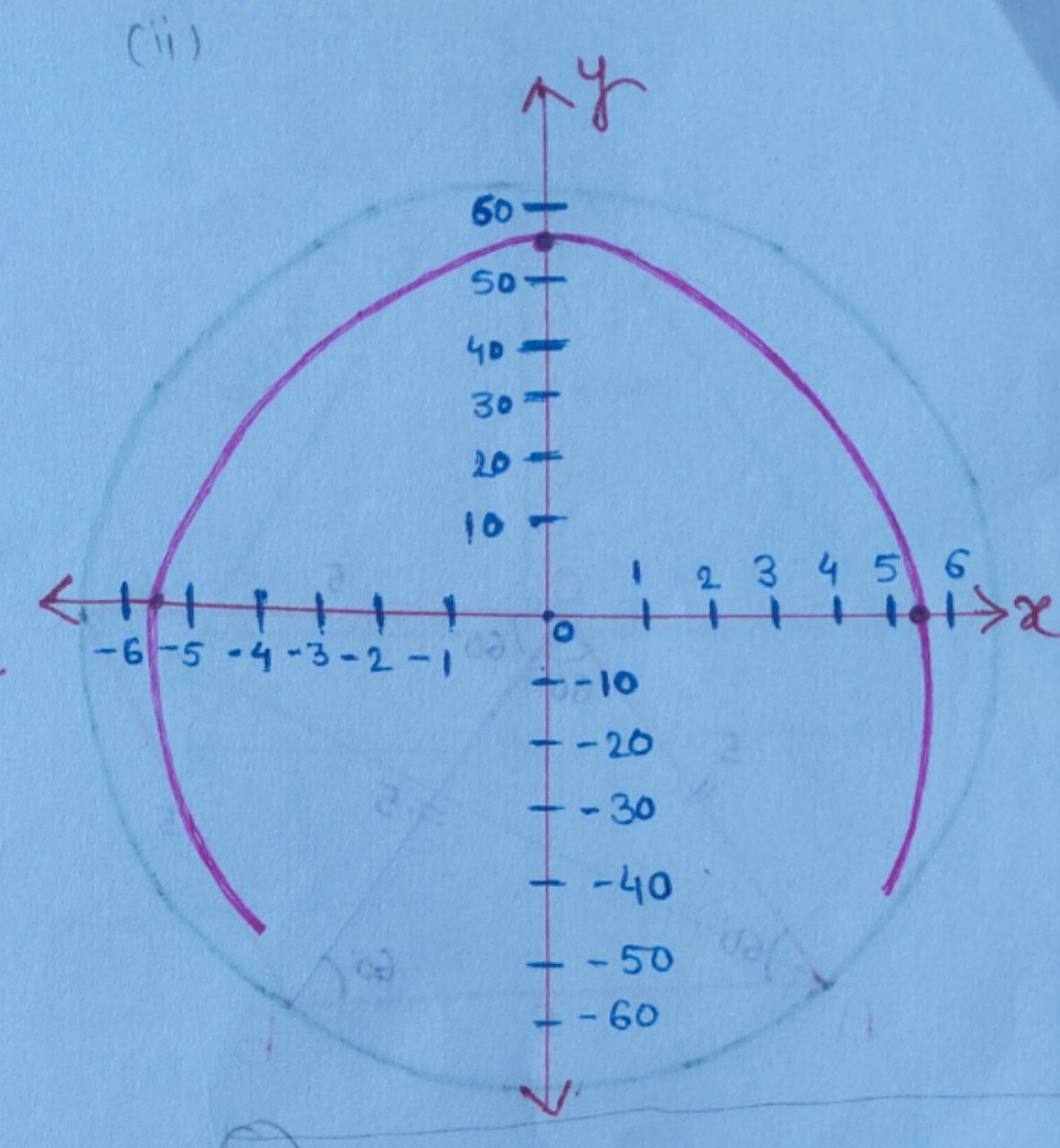
$ y_{2} = 52 – 2x^{2}$ is a quadractic equation.

$ y_{2} = 0 \Rightarrow x = \sqrt{26} = \pm 5 \cdot 09 $

$ x = 0 \Rightarrow y_{2} = 52 $

Now, combine both graphs, we get

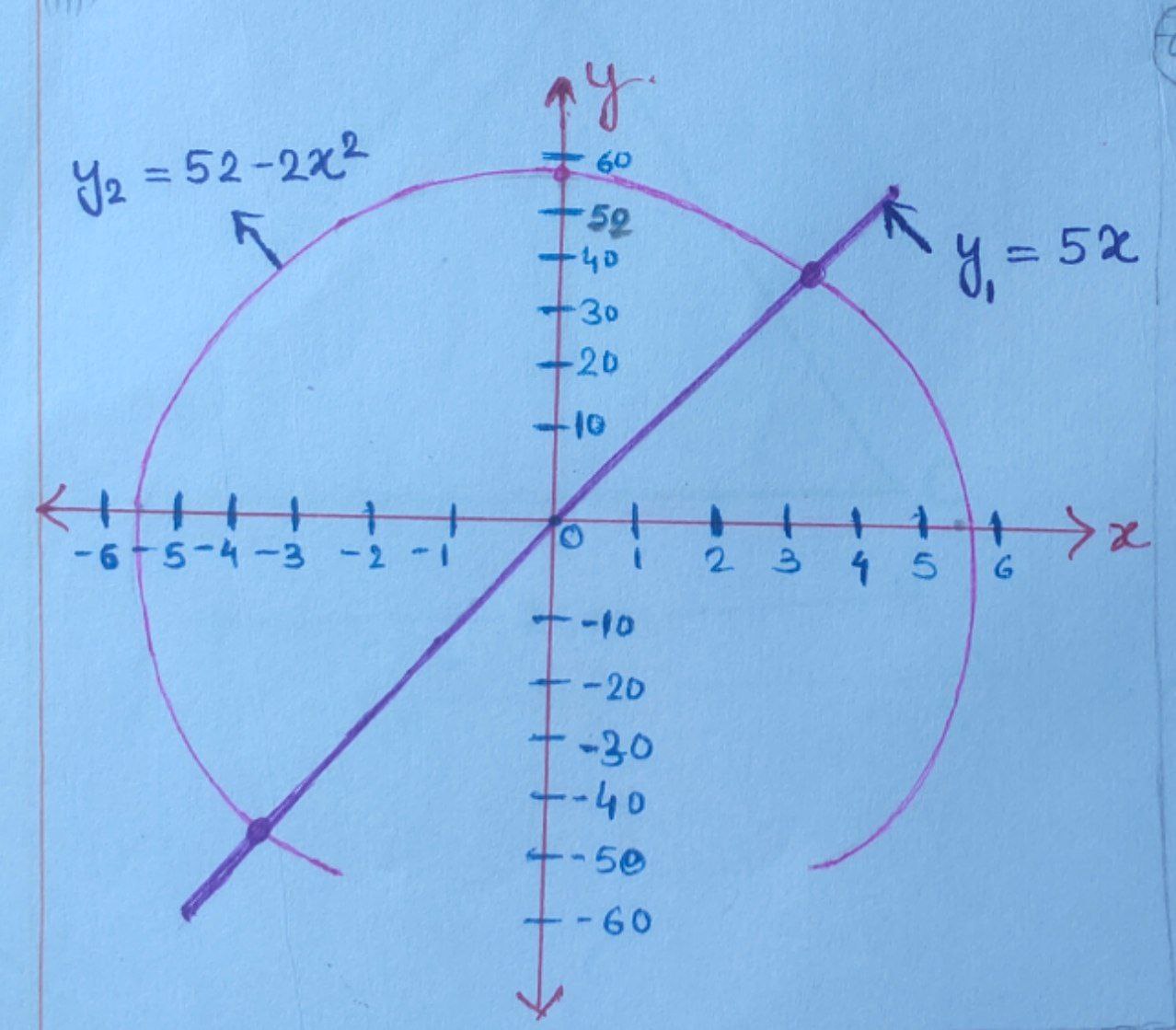
From the above graph,

$ 5x = 52 – 2x^{2} $

$ \Rightarrow – 2x^{2} + 52 – 5x = 0 $

$ \Rightarrow 2x^{2} + 5x – 52 = 0 $

$ \Rightarrow 2x^{2} + 13x – 8x – 52 = 0 $

$ \Rightarrow x( 2x+13) – 4(2x+13) = 0 $

$ \Rightarrow (2x+13) (x-4) = 0 $

$ \Rightarrow 2x+13 = o , x-4 = 0 $

$ \Rightarrow \boxed{x = \frac{-13}{4}} ,  \boxed{x=4}$

Since, $x$ is positive real number, so we take $x = 4.$

Now, from equation $(1),$

$ f(x) = \max \{ 5(4), 52 – 2(4)^{2} \}$

$ \Rightarrow f(x) = \max \{ 20, 52 – 32 \} $

$ \Rightarrow f(x) = \max \{ 20, 20 \} $

$ \Rightarrow \boxed{f(x) = 20} $

$\therefore$ The minimum possible value of $f(x)$ is $20.$

Correct Answer $: 20 $