Consider a cylinder of height $h$ cms and radius $r=\frac{2}{\pi}$ cms as shown in the figure (not drawn to scale). A string of a certain length, when wound on its cylindrical surface, starting at point A and ending at point B, gives a maximum of $n$ turns (in other words, the string‟s length is the minimum length required to wind $n$ turns.)
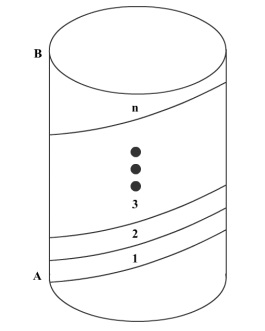
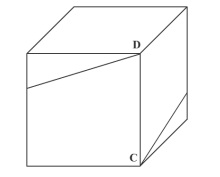
The same string, when wound on the exterior four walls of a cube of side $n$ cms, starting at point C and ending at point D, can give exactly one turn (see figure, not drawn to scale). The length of the string, in cms, is
- $\sqrt{2}n$
- $\sqrt{12}n$
- $n$
- $\sqrt{13}n$